Batch 3 - Class 158 - Right Angled Triangles, Hamiltonian Cycles
Attendance Muskaan, Arnav, Anishka, Liza, Damini, Arjun
Class puzzles
Right Angled Triangles
- Find the right angled triangle with integer sides, and the largest perimeter, with one of the sides measuring 12 units
- For younger kids, as them to find the triangle if one of the sides measures 4 units. How about 6 units?
- How do you know that this is indeed the largest such triangle? Can you prove that?
- Generalize the above - is this valid for all numbers?
- All even numbers?
- Is there a integer-sided right angled triangle for each integer as one of its sides?
- Can you prove that?
- Is it possible that some integers don't fit into the Pythagoras triplets?
- Is there an integer sided right angled triangle for each integer as its hypotenuse?
- Can you find the largest such triangle if one of the sides is 13?
- For younger kids, how about if the side is 3 units? 5 units?
- How do you know that this is indeed the largest such triangle? Can you prove that?
- For a given side, say 27, how many right angled triangles exist with 27 as a minor side?
- If you take one side as 27, then for other sides a and b, (a+b)(a-b)=27.27
- If you take any two unique factor pairs of 27.27, you get two simultaneous linear equations. Each of those will have a solution corresponding to a right angled triangle.
Hamiltonian Cycles
Revision: Hamiltonian cycles are cycles which go through each vertex of a graph exactly once, and then return to the starting vertex. Lets try to create graphs where some of the edges are given, and we will try to complete the graph so that it has a hamiltonian cycle. Edges can only be drawn horizontally or vertically.
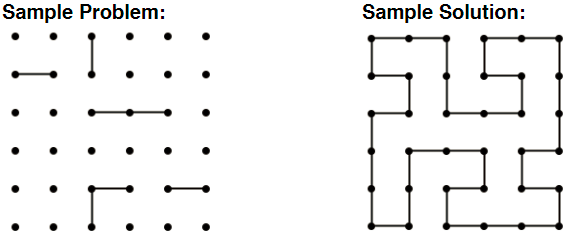
Notes:
- Each problem has only one solution, so don't guess
- Since each vertex can only be entered and exited once, how many edges must it have? Can you start with some edges that are obvious and then move out.
- If an edge creates a partial cycle without covering all vertices, then it can be ruled out
- If some edge "isolates" another vertex, then it can be ruled out
(Give worksheet for each kid to solve)
Homework Problem:
- Complete the Hamiltonian cycle puzzles above
References: